Proofs about programs
An interactive tutorial
The halting problem be damned — we can prove all kinds of things about programs, and we can even check those proofs with computers! In this chapter, we’ll use a language called Lean to prove whether the famous Ackermann function always halts. Along the way, we’ll introduce Noetherian induction and formal systems.
To warm up, here’s a JavaScript function called fac:
function fac(n) {
if (n <= 0) return 1;
else return n * fac(n-1);
}If we run fac(0), will it halt?
Right, it will immediately return 1.
Actually, it will halt: the test 0 <= 0 passes, so it immediately returns 1.
But what about fac(1), will that halt?
Right, it will return 1 * fac(0), which is 1 * 1, which is 1.
No, this too will halt. The test 1 <= 0 fails, so it calls itself, returning 1 * fac(0). We just saw that fac(0) returns 1, so this reduces to 1 * 1, so the whole thing returns 1.
But what about fac(42)?
Fine, fine! But this illustrates something important. You didn’t just run fac(42) in your head — instead you just figured, “I can see that fac(n) halts, whatever n is.” But how did you prove that to yourself?
Mathematical induction 🍳
Let’s play the game once more, but this time for a function bar. This time, I won’t show you the source code for bar; I’ll just tell you two things about it:
Fact 1: bar(0) halts.
Fact 2: If bar(n) halts, then bar(n+1) halts.
Does bar(55378008) halt?
Indeed, we can use fact #2 to conclude that bar(1) halts, then use it again to conclude that bar(2) halts, et cetera, all the way up to bar(55378008).
I would argue it does halt. We’re told that bar(0) halts. Then, using fact #2, we can conclude that bar(0+1) halts, i.e. bar(1) halts. Using fact #2 again, we can conclude that bar(1+1) halts. Using fact #2 another 55,378,006 times, we can conclude that bar(55378008) halts.
Let’s generalize this. We’ll say H(n) means “the function bar halts on input n”. Then the first fact says H(0), and we call this the “base case”. And the second fact says H(n) implies H(n+1), and we call this the “induction step”.
Then let’s say we want to prove H(4). We can do so by starting with the base case, and applying the induction step four times:
Is H(n) true for every natural number n?
The same works for any other meaning of H, and is a common way to prove a “for all” statement:
🔐 Unlocked: Proof by Induction
If P(0), and if P(n) implies P(n+1), then P holds for every natural number n.
Once more, in Lean
So, induction is one way to prove to ourselves that a program halts. But what about proving it to the computer? Enter Lean 4, a language that lets us prove things about our programs.
Here’s fac again, but rewritten in Lean:
def fac: Nat -> Nat
| 0 => 1
| n+1 => (n+1) * fac nYou don’t need to understand it all, but you can read it if you squint. Nat means “natural number”, i.e. the numbers 0, 1, 2 and so on. And the | n+1 => says, “if the input number looks like n+1, return the following”.
If you copy-paste this into a file and run lean on it, congratulations! You’ve written your first computer-verified proof that a program halts!
That’s because Lean only lets you write functions that halt. And Lean accepts the above program without trouble, by saying: “I can see that fac 0 halts. And I can see that fac (n+1) halts if fac n halts. So by induction, fac n must halt for any n. I therefore accept this function definition.”
The Ackermann function ♾️
Let’s try a famous tricky function called the Ackermann function:
function ack(m, n) {
if (m === 0) return n+1;
else if (n === 0) return ack(m-1, 1);
else return ack(m-1, ack(m, n-1));
}Does this function always halt? Try out a small example: what is ack(1,1)?
That was a bit of work! But not too hard.
No, it’s 3, and here’s how we could compute it:
ack(1, 1) =
ack(0, ack(1, 0)) =
ack(0, ack(0, 1)) =
ack(0, 2) =
3Next, let’s look at ack(4,2).
No! Wait! Come back! The last student that tried it was found dead, crushed under piles of notepaper and Red Bull!
We should convince ourselves that our programs will halt before we go off calculating them. Luckily, we have a way to test this! We can just ask Lean:
def ack : Nat -> Nat -> Nat
| 0 , n => n+1
| m+1 , 0 => ack m 1
| m+1 , n+1 => ack m (ack (m+1) n)Unfortunately, running Lean on this file, it complains:
failed to prove terminationDarn! Does that mean ack doesn’t halt?
No — Lean says it failed to prove that it does halt, but that’s different from proving that it doesn’t halt. Lean is just saying: “try harder; I’m not yet convinced.”
Indeed, Lean didn’t prove that it doesn’t halt. We’re just going to have to think harder.
Here’s a way to visualize what ack is doing. We can write out its values in a spreadsheet:
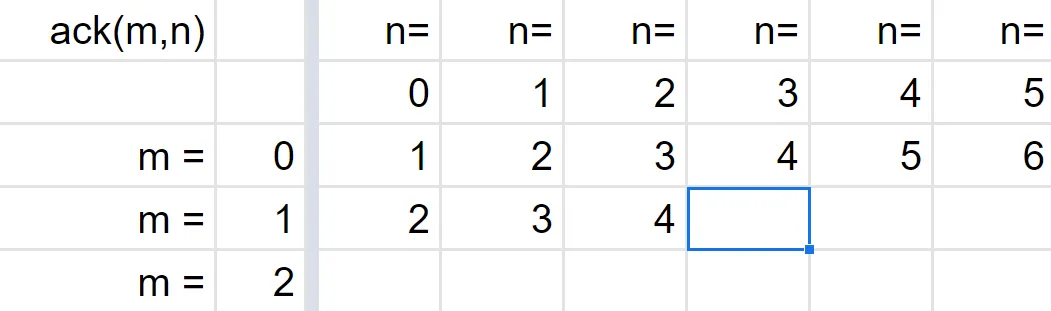
Above, we’ve got the first argument m down the side, and the second argument n along the top. We’re filling in the cells in normal reading order: row by row, and each row left to right. Now here’s the ack algorithm in English: “To fill in a cell, take the value of the cell to the left, and use it as an index into the row above.”
For example, we just filled in ack(1,2). We looked at the cell to the left, which has value 3. Then we looked at the row above, and took the cell at index 3, i.e. ack(0,3). That cell has value 4, so that’s our answer.
Our next cell to fill in is ack(1, 3). What’s its value?
No, it’s 5. We first look at the value of the previous cell, which is 4. Then we look up index 4 from the row above, i.e. row 0. That cell has value 5, so that’s the answer.
Right, we take index 4 from row 0.
Perhaps now you’re seeing an argument that ack always halts? Completing the table in normal reading/writing order, each cell only uses previous cells: the cell to the left, and a cell in the row above.
So, perhaps we can apply induction, just like we did with fac: “ack halts for cell 0. And if it halts for cells 0…n, it will halt for cell n+1. So it will halt for all cells.”
This argument is actually using a variant of induction called complete induction:
🔐 Unlocked: Complete Induction
If we can show P(n) from the assumption that P(m) for every m<n,
Then we can conclude that P(n) for every n.
To apply this argument, we need to number the cells in our spreadsheet. The first cell ack(0,0) has cell number 0. The cell ack(0,1) has cell number 1.
What is the cell number of ack(1,0)?
Yeah ... the problem is that our cells are in an infinite grid, not a line. So assigning every cell a number doesn’t work (at least, not in reading order). Also, we conveniently imagined that we’d completed the first row, even though that would take forever!
This is why Lean didn’t accept our definition of ack: ordinary induction doesn’t work.
Noetherian induction
Enter Emmy Noether. She improved the induction method so that we don’t have to number everything.
We can draw a graph of the data flow in our spreadsheet. Here’s the graph for ack(2,1):
We can explore ack(2,1)’s call stack by starting at the red box (function call), and following arrows backwards. The green boxes are ‘base cases’, which have no recursive function calls, and therefore no arrows into them.
Is it possible to follow arrows backwards from ack(2,1), but never reach a green box?
I think you always reach a green box. For example, going from (2,1) to (1,3) to (1,2) to (0,3) reaches a green box. If you can find a counter example in that diagram, email me!
That should make it clear that ack(2,1) halts. Now, here are the data flow graphs for four unknown function calls. Which one halts?
Right! All the others have loops, or infinite recursion.
No, C doesn’t halt. It never “loops,” but it recurses forever, never reaching a base case. Only D has the correct structure.
No, B doesn’t halt: after four levels of recursion, it calls itself again, in an infinite loop. Only D has the correct structure.
No, A doesn’t halt, because it makes a function call that then calls itself in a loop. Only D has the correct structure.
We want to convince Lean that, for any m and n, ack(m,n) always has a graph with that property: that you’ll always reach a base case within a finite number of steps.
Well-ordering
Let’s return to our earlier argument: we argued that ack always halts because “each cell only uses previous cells”. This doesn’t require numbering all the cells; it just requires some definition of “previous”. The definition we’re using is: “previous by normal reading order”: check the row number first, then tie-break using the column number.
We write this relation with <, just like with ordinary numbers. For example, which of these is true?
No, (3,3) is not less than (2,9). To compare them, we first compare the first number. We find that 2 < 3, so (2,9) < (3,3).
Emmy Noether said: you can consider this relation, (a,b) < (c,d) to have a graph, too! Here, an arrow from box a to box b means that a<b:
Imagine starting at a random box in this infinite graph — say, (5,42). Then repeatedly follow arrows backwards from it to a “previous” box. Will you always eventually reach the box (0,0)?
I think you will. Imagine, starting at, say, (m=4,n=23), and trying to avoid hitting (0,0) for as long as possible. We can decrease n until we get to (m=4,n=0). But then we have to go to m=3. We could pick, say, n=99999 or some other large number — but we’ll always go back to some finite number. Then after 99,999 steps, we’ll have to go back to m=2. Et cetera.
A mathematician might say that “< is a well-founded relation on pairs of natural numbers.” This is just a fancy way to say that you’ll always reach (0,0).
We can now make another attempt at a formal argument that ack always halts: “Pick any ack(m,n). By following its function calls, we’re really just following paths through the < graph on pairs of numbers. And because that always halts, ack(m,n) must halt, too.”
Lean understands this kind of argument! We can prove to Lean that our function halts, by appending:
termination_by ack m n => (m, n)Lean reads this and thinks: “Okay, you’re telling me to associate each function call ack m n with the pair of numbers (m,n). I know about < on pairs of numbers. And I know that this relation is ‘well-founded.’ And I can see that each call to ack follows this relation backwards to a smaller pair of numbers. I therefore accept that this function always halts.”
🔐 Unlocked: Noetherian induction
Given some well-founded relation a<b,
if we can show P(x) from the assumption that P(y) for every y<x,
then we can conclude that P(x) for every x.
(You might notice that the above is the same as complete induction, just generalizing from natural numbers to anything where we can define “less than”.)
Proving machines halt 🤚
So this is how we can prove that Lean functions halt. But what if we want to talk about other models of computing — say, Turing machines, or JavaScript? Can we talk about those in Lean?
Yes! We can write an interpreter for the language we care about, then prove things about the interpreter. Here’s an extremely restricted form of computer in JavaScript:
function step(state) {
switch (state) {
case "A": return "B";
case "B": return "Halt";
case "C": return "D";
case "D": return "C";
case "Halt": return "Halt";
}
}To run this useless computer, you repeatedly apply the step function until reaching the Halt state.
Consider starting with state A, and repeatedly applying the step function. Does it eventually reach the Halt state?
No, it will halt, after two steps: after A, it steps to B, and then from B, it steps to Halt.
What about starting with state C? Will that reach the Halt state?
I think it won’t halt. After C, it steps to D. But then from D, it steps back to C again. Then this cycle repeats forever, never reaching the Halt state.
So, if you need to heat your house, start with C or D! But can we prove this to Lean? First, we have to translate the program into Lean:
inductive State where
| A | B | C | D | Halt
def step : State -> State
| A => B
| B => Halt
| C => D
| D => C
| Halt => HaltRecall that Lean only accepts a function definition if it can see that it always halts. Will Lean accept our definition of step?
Right, step has no recursive calls — or indeed, any function calls at all — so it’s easy to see that it halts.
This is a bit tricky. Lean will accept step, because it has no recursive calls — or indeed, any function calls at all. For example, step C immediately halts, returning D. Note that Lean has no clue here that we’re intending to iterate the step function, and has nothing to say on whether that will halt.
Next, we have say what it means to run this machine. This function runs it for n steps:
def run : Nat -> State -> State
| 0, s => s
| n+1, s => step (run n s)What is run 42 A?
No, it’s Halt. Notice that the Halt state just loops back to Halt. For run 42 A, it follows the series A → B → Halt → Halt → ..., so for any n greater than 1, the state will be Halt.
(Note in passing that Lean accepts the definition of run. Why? Because it can see that n always decreases.)
So far, we’ve used Lean as a programming language — but Lean is also a formal system that lets us makes logical propositions and prove them. Here’s our first proposition:
def A_halts_prop: Prop :=
exists n: Nat, run n A = HaltThis says, “A_halts_prop is the proposition that there exists some number n such that run n A equals the Halt state.”
Note this doesn't prove it! It just makes the claim, and we can claim all kinds of false things! However, is this proposition true?
Indeed, it’s true. This proposition is just saying, “run n A halts,” and it does so after just two steps.
No, I would say it’s true: there does exist such an n, for example, n = 2. That is, after 2 steps, it will reach the Halt state.
To prove the proposition that an n exists, one way is just to provide such an n, like n = 2. And we can write this proof in Lean:
theorem A_halts : A_halts_prop := by
exists 2To check this proof, Lean evaluates run 2 A, then checks that it equals Halt. It does, so it accepts our proof.
What would have happened if we wrote exists 999999999 instead?
Right — it would just take a bit longer to evaluate! 🙂
No, Lean would still accept the proof, but it would take longer. It would evaluate run 999999999 A, which eventually yields the value Halt.
Proving programs don’t halt ➿
We’ve spent all this time proving that programs do halt, but what if we want to prove that a program does not halt? This ability will be important in our next chapter on Gödel’s incompleteness theorem.
Here’s the step function again, this time as a diagram:
Just like before, we can propose that the machine halts when running from C:
def C_halts_prop: Prop :=
exists n: Nat, run n C = HaltWill Lean accept this definition?
Right, we’re not yet saying anything about whether the proposition is true, we’re just giving it a name.
This is tricky — Lean actually will accept this definition! The thing is, we’re not yet saying anything about whether the proposition is true, we’re just giving it a name.
But yes, the proposition is false, so we actually want to propose that there does not exist any n such that run n C is the Halt state:
def C_hangs_prop :=
¬ exists n: Nat, run n C = HaltTo prove that a program does halt, we basically told Lean: “Just run it! You’ll see!” Can we use the same approach to prove that a program doesn’t halt?
Right, it’s a bit trickier.
No, we can’t — if the program doesn’t halt, then running it will never halt. Remember also that Lean will only run something if it knows beforehand that it will halt.
To prove this one, we’ll have to go back to our friend, induction. Remember that induction lets us prove that something is true for all values. Therefore, we need to change our proposition a bit, so that instead of saying ¬ exists n, we instead say forall n:
def C_hangs_prop :=
forall n: Nat, run n C ≠ HaltThis says, “for every natural number n, run n C does not equal the Halt state.” Is this equivalent to our previous proposition?
I would say it’s equivalent. Generally, “for all x, it’s not the case that P(x)” is equivalent to saying “there does not exist an x such that P(x)”.
Now here’s an attempt at proving this by induction:
Base case: If we started at C, the first state was not Halt.
Induction step: If we started at C, and the current state is not Halt, the next state will not be Halt either.
Read the induction step carefully! If you have a state that is not Halt, does it follow that the next state is not Halt?
The problem here is that our induction hypothesis, “the current state is not Halt”, is not enough to conclude that the next state is not Halt. For example, maybe the current state is B — then the next state would be Halt.
We need more information in the induction step. So here’s a second attempt at a proof by induction:
Base case: If we started at C, the first state was either C or D.
Induction step: If we started at C, and the current state is C or D, then the next state will either be C or D.
Again, read the induction step carefully! Can we prove it?
This time, the induction hypothesis is strong enough to let us prove the induction step. We can say, “well, if it’s C, the next state will be D. And otherwise if it’s D, then the next state will be C.”
🔐 Unlocked: Strengthening the induction hypothesis
If your proof is failing at the induction step, it might be easier to prove something stronger!
This principle can be counter-intuitive! It’s usually harder to prove something stronger, but when using induction, it can actually be easier.
Here’s the stronger theorem that we informally proved: “starting from C, every future state will be either C or D.” And here’s that proof written in Lean — but you don’t need to understand it all:
theorem C_D_loop:
forall n,
run n C = C ∨ run n C = D
:= by
intro n
induction n with
| zero => apply Or.inl; rw [run]
| succ n ih =>
cases ih with
| inl hc => apply Or.inr; rw [run, step, hc]
| inr hd => apply Or.inl; rw [run, step, hd]Using this theorem, we can weaken it to prove that the machine does not halt from C. We just observe that neither of C or D are the Halt state:
theorem C_hangs: C_hangs_prop := by
intro n
have is_c_or_d := C_D_loop n
cases is_c_or_d with
| inl is_c => rw [is_c]; simp
| inr is_d => rw [is_d]; simpConclusion
From here, we could add features like “input”, “output”, and “memory”. We’d quickly get to Turing Machines. We could go further, modelling JavaScript, or even Lean itself. To reason about them, the same principles will apply: somehow prove whether or not there exists some n:Nat such that the program will halt after n steps.
In this chapter, you’ve learned how to prove things using induction, and you’ve learned how to use this technique in Lean, to prove whether programs halt or not. Perhaps you’re wondering — just how much can I prove in Lean? Are there things it can’t prove? In the next chapter, you’ll learn Gödel’s first incompleteness theorem: a famous result that says, yes, for any formal system like Lean, there are true things that it cannot prove.
Endnotes
This chapter is free this week! If you like it and want to read the other chapters, please consider supporting me by buying the course!
Other reading material:
Here’s a nice intro to Noetherian induction by Joseph Sullivan.
Read more about theorem proving in Lean 4.
The Natural Number Game is super fun, although it’s for Lean 3.